Урок 8. Примеры использования рекурсии

[admin.guide]

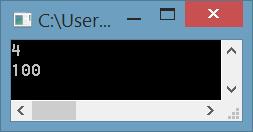
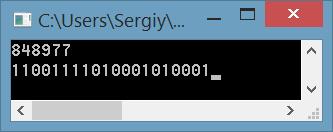
Вывод в двоичном формате положительного числа, переданного в десятичном формате

static void Converter(int n)
{
    int temp;

    temp = n % 2;
    
    if (n >= 2)
        Converter(n / 2);

    Console.Write(temp);
}

static void Main()
{
    int n = Convert.ToInt32(Console.ReadLine());

    Converter(n);

    Console.ReadKey();
}

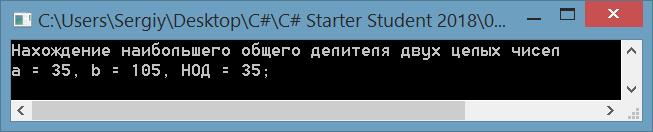
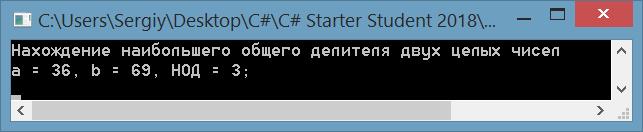
Нахождение наибольшего общего делителя (НОД) двух целых чисел

static int Calculate(int a, int b)
{
    if (a % b == 0)
        return b;
    else
        return Calculate(b, a % b);
}

static void Main()
{
    Console.WriteLine("Нахождение наибольшего общего делителя двух целых чисел");

    int a = 35, b = 105;

    Console.WriteLine("a = {0}, b = {1}, НОД = {2};", a, b, Calculate(a, b));

    Console.ReadKey();
}

// Второй вариант решения (без использования рекурсии)
static int Calculate2(int a, int b)
{
    while (b != 0)
        b = a % (a = b);
    return a;
}

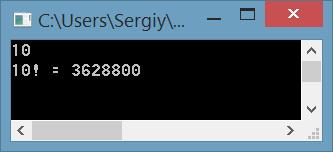
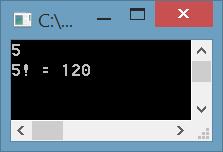
Нахождение факториала числа (n!)

static int Factorial(int n)
{
    if (n == 0)
        return 1;
    else 
        return n * Factorial(n - 1);
}

static void Main()
{            
    int n = Convert.ToInt32(Console.ReadLine());

    Console.WriteLine($"{n}! = {Factorial(n)}");

    // Задержка.
    Console.ReadKey();
}

Примечание: рекурсию ненужно применять во всевозможных задачах. Её нужно применять только в ситуациях, когда она сильно упрощает написание кода или же без неё решить поставленную задачу невозможно. Одной из задач, когда нужно применить рекурсию является вывод дерева папок существующих в системе (поскольку без её использования нужно будет написать очень много циклов (около 8000 для ОС Windows)). Вторым примером является реализация сортировки массива, с неизвестным количеством элементов, используя алгоритм быстрой сортировки.

Источник: видеоурок Александра Шевчука "МЕТОДЫ. РЕКУРСИЯ"

предыдущая статья | следующая статья